建模与高斯的区别 阐述高斯混合模型及其适用场景

课程体系高斯数学是将小学课内课外数学囊括其中建模与高斯的区别，并形成横向7大板块以及纵向6个年级的知识树体系的小学尖端数学课程教育理念高斯数学的教育理念是通过学习数学发展脑区功能，培养终身受用的思维它强调数学思维的本质是建模，即把日常生活中遇到的问题翻译为数学问题，并用数学方法推导出决策模型，然后；在图像处理领域，高斯模型可以用于背景建模图像灰度直方图反映了灰度值在图像中的频率分布，可以视为对图像灰度概率密度的估计对于具有显著差异的目标区域和背景区域，直方图会呈现出双峰结构，每个峰值分别对应于目标和背景的中心灰度值对于多峰的复杂图像，如医学图像，可以将这种多峰特性视为多个高斯。

1两者的区别在于高斯数学是专门培养孩子们的学习方法和解题思路的，而奥数是专门培养孩子们的思维方式 2高斯数学和奥数本质是一样的，都是一种教学方式，高斯数学和奥数都是一种很不错的教学模式 扩展资料 1通过学习数学发展脑区功能，培养终身受用的思维 2事事皆数学建模数学思维的本质是建模，把日；概念高斯过程是一种概率统计方法，它非参数地直接对函数进行建模应用在机器学习中，高斯过程广泛应用于各种领域，如超参数优化等优势能够灵活模拟复杂函数，并量化不确定性，适用于处理大量随机参数和复杂建模需求高斯过程的数学基础无限维高斯分布高斯过程的核心是无限维高斯分布，它将输入。

简而言之，无论是高斯分布还是正态分布，它们都是描述数据分布的一种重要工具，具有广泛的应用价值在统计学和数据分析中，建模与高斯的区别我们常常利用正态分布的特性进行数据分析和建模，帮助人们更好地理解和预测各种现象的变化趋势虽然两者在某些情况下可能被用来表示不同的具体分布情况，但在大多数情况下可以视为。

建模与高斯的区别是什么

应用高斯过程在估计和不确定性分析中有着广泛应用，特别是在高斯过程回归中通过观测数据，可以推断出未观测参数处的随机变量分布，实现数据驱动的预测和分析总结联合高斯分布和高斯过程在概率建模中具有不同但互补的应用联合高斯分布适用于多变量概率分布建模，而高斯过程则适用于随机过程建模，通过。

1高斯数学是“北京？广州超常儿童教育研究中心”在小学数学领域的重点研发和推广课题，该课题起步于上世纪90年代，于2001年在的带领下形成体系，开创了国内超常儿童教育向公立体制外拓展的先河自那时起，高斯数学一直引领国内数学课外教育的发展潮流和方向2课题简介高斯数学是将小学课内课外数学囊括。

高斯噪声是概率密度函数服从高斯分布的一类噪声，常在传感器长期工作热度过高或电路元器件自身及相互影响时产生泊松噪声符合泊松分布的噪声模型，通常由于光子击中传感器后产生的电流电压带有这种噪声，也称为散粒噪声椒盐噪声是黑白相间的亮暗点噪声，来源于图像传感器传输信道和解码处理过程对噪声进行建模。

高斯数学的教育理念强调通过学习数学发展脑区功能，培养终身受益的思维能力其课程设计注重将数学建模融入日常生活，从日常生活中的小事如上下班路线选择，到长远的年度规划，都是数学建模的应用从小学好数学，不仅是为了应对考试和竞赛，更是为了培养良好的思维能力，提高逻辑推理归纳分析空间想象数字。

高斯模型是一种数学工具，它利用高斯概率密度函数，也就是著名的正态分布曲线，对现实世界中的事物进行建模和量化这个模型通过将复杂现象分解为多个相对独立的高斯分布，每个分布代表事物的一个特征或特性值的分布情况在图像处理领域，以背景建模为例，图像灰度直方图反映了灰度值在图像中的频率分布，可以。

高斯数学是quot北京#9642广州超常儿童教育研究中心quot在小学数学领域的重点研发和推广课题，该课题起步于上世纪90年代而奥数起源于1934年在列宁格勒4教育理念高斯数学以数学为工具，辅以有趣的蕴含数学思想的益智游戏边玩边学，增强孩子对数学的探究兴趣动手能力和空间想象力因此高斯的数学课堂区别。

是“高斯杯”全国大学生数学建模挑战赛的目的在于拓宽学生视野，激励学生培养数学建模的能力，培养学生创新精神的学科竞赛，搭建展现学生学科基础的平台，提高学生运用理论知识解决社会热点与生活问题的能力，扩大学生科研视野同时鼓励广大学生踊跃参加课外科技活动，培养创造精神及合作意识。

高斯杯数学建模竞赛含金量

4 数据分类和异常检测GMM可以用于数据分类和异常检测通过判断观测数据属于哪个单高斯分布，从而对数据进行分类同时，GMM首先对观测数据进行多高斯分布建模，并通过EM算法估计单高斯分布参数，如果测试数据在隶属的高斯分布中的概率密度值小于阈值，则判定为异常点5 图像生成GMM能够用于图像生成。

高斯数学是北京广州超常儿童教育研究中心在小学数学领域的重点研发和推广课题以下是关于高斯数学的详细解释起源与发展高斯数学起步于上世纪90年代，于2001年形成体系它开创了国内超常儿童教育向公立体制外拓展的先河，并一直引领国内数学课外教育的发展潮流和方向数学思维本质数学思维的本质是建模，即。

例如，在金融领域，股票价格收益率等经济指标的波动往往呈现出正态分布的特征，通过高斯模型可以分析这些波动并做出投资决策此外，在图像处理信号处理等领域中，高斯模型也发挥着重要的作用通过对图像或信号进行高斯建模和分析，可以提高图像或信号处理的效率和质量总之，高斯模型是一种重要的数学工具。

GMM，高斯混合模型，也可以简写为MOG高斯模型就是用高斯概率密度函数正态分布曲线精确地量化事物，将一个事物分解为若干的基于高斯概率密度函数正态分布曲线形成的模型。

关于这个问题，FA因子分析和GP高斯过程是两种常用的统计建模方法，它们在应用和原理上有一些区别1 应用领域 FA主要用于数据降维和发现潜在因子之间的关系它是一种无监督学习方法，常用于心理学社会科学等领域 GP主要用于回归和分类问题它是一种基于概率的监督学习方法，常用于机器。

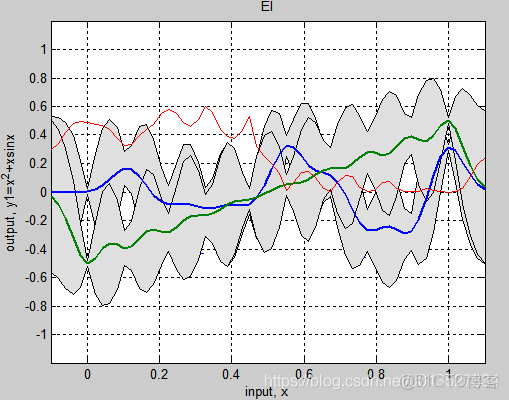
高斯模型就是用高斯概率密度函数正态分布曲线精确地量化事物，将一个事物分解为若干的基于高斯概率密度函数正态分布曲线形成的模型对图像背景建立高斯模型的原理及过程图像灰度直方图反映的是图像中某个灰度值出现的频次，也可以以为是图像灰度概率密度的估计如果图像所包含的目标区域和背景区域相差。